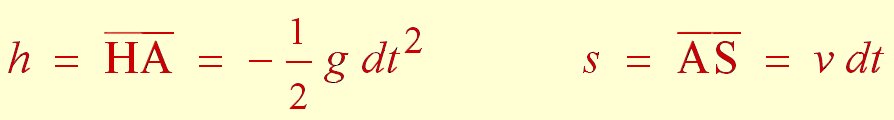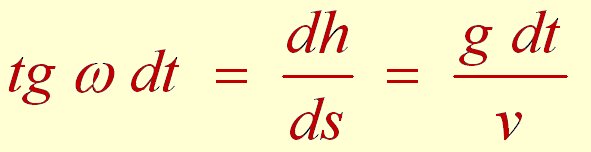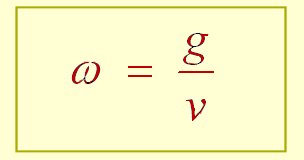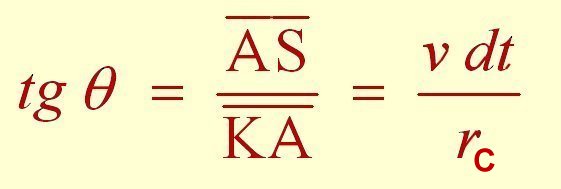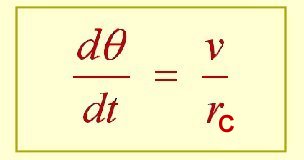|
Raisonnons dans l'espace-temps apparent, celui qui nous est habituel, et observons
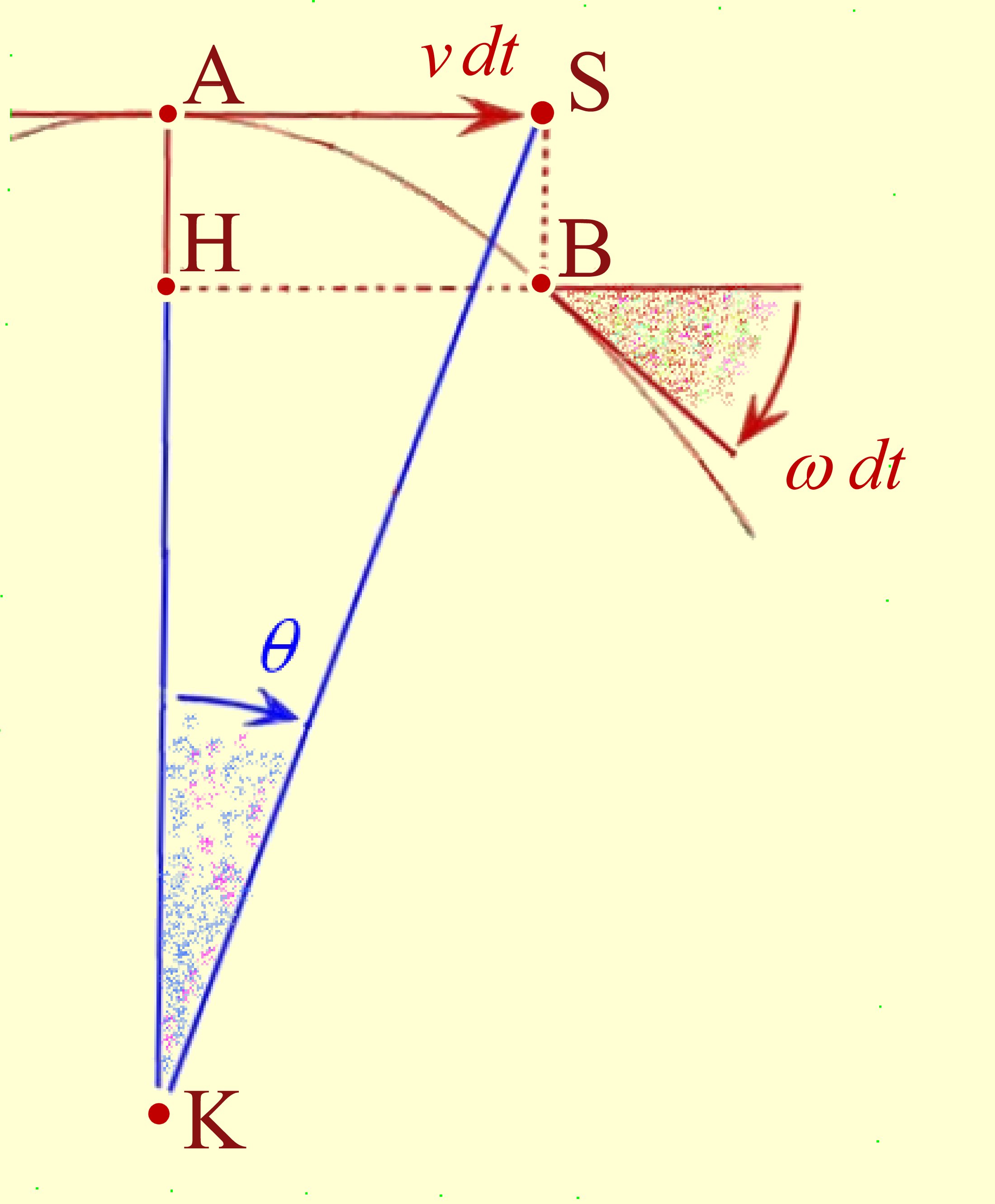
un objet passant par un point
A
de l'espace, avec une certaine vitesse
v
, perpendiculaire à la direction
AH
de l'accélération. Observée sur un court intervalle de temps
dt
sa trajectoire est assimilable à un arc de parabole
AB
qui répond aux formules :
|
|
La
rotation
est l'angle dont tourne le vecteur vitesse :
|
|
À la limite lorsque la durée
dt
tend vers 0 :
|
|
Par ailleurs, c'est au centre cinétique
K
qu'il faut se poster pour mesurer les
vitesses angulaires.
|
Les rotations et les
vitesses angulaires
sont des grandeurs
différentes.
|